A* Pathfinding in Videospielen

Pathfinding (Wegfindung) ist in Videospielen ein Thema mit langer Tradition. Immer wenn ein Charakter sich von einem Punkt zu einem anderen Punkt bewegen möchte, muss in irgendeiner Weise evaluiert werden, wie dieses Vorhaben ohne Kollisionen mit der Umwelt geschieht. An diesem Punkt kommt die Wegfindung in's Spiel. Im folgenden Beitrag wird auf die Verwendung des A*-Algorithmus für geografische Wegfindung eingegangen.

Entwickler und Entwicklerinnen verwenden den A*-Suchalgorithmus, um bei einer Wegfindung-Problemstellung (Pathfinding-Problemstellung) den günstigsten Weg vom einen zu anderen Punkt zu finden. Der Algorithmus ist im Einsatzgebiet der geografischen Wegfindung bei Spielen einer der beliebtesten, weil er gemessen an der geringen Komplexität eine große Effizienz aufweist. Bei einer sehr hohen Anzahl von Agenten kann es trotzdem zu Performance-Problemen der CPU kommen.

Eine hinreichende Voraussetzung ist, dass die Spielwelt durch ein Punktraster eingeteilt wird. Es kann sich dabei um ein zwei- oder auch dreidimensionales Raster handeln. In beiden Fällen sollte die Größe der Rasterpunkte jedoch mit Bedacht gewählt und gegebenenfalls im Bezug zur Spielwelt vereinfacht werden. In einer großen, prozedural generierte Spielwelt mit einem hohen Detailgrad, in welcher Einheiten stetige Koordinaten einnehmen können, wäre der Suchraum für eine heuristische Suche zu performancelastig. Dem entsprechend eignen sich Spiele, welche eine vereinfachte, rasterisierte Spielwelt verwenden, am besten für A*-Wegfindung.

In diesem Fall blockieren Objekte diskrete Rasterpunkte: Entweder ein Objekt blockiert den Rasterpunkt oder nicht. Bei einem Punkt A beginnend, untersucht der Algorithmus die acht an A benachbarten Rasterpunkte (folgend Knotenpunkten oder auch Knoten genannt) aufgrund ihrer Kosten, um zum Zielknoten B zu gelangen.

f(x) = g(x) + h(x)

Um die Kosten zu berechnen wird eine Metrik f(x) verwendet. Für den Knoten x beschreibt g(x) die Summe der Kosten, um zu diesem Knoten zu gelangen und h(x) die geschätzten Kosten, um zum Ziel zu kommen. Wobei eine horizontale und vertikale Bewegung in der Regel mit 10 und eine diagonale Bewegung mit 14 gewichtet wird. Den Ursprung haben diese Gewichtungen im Satz des Pythagoras.

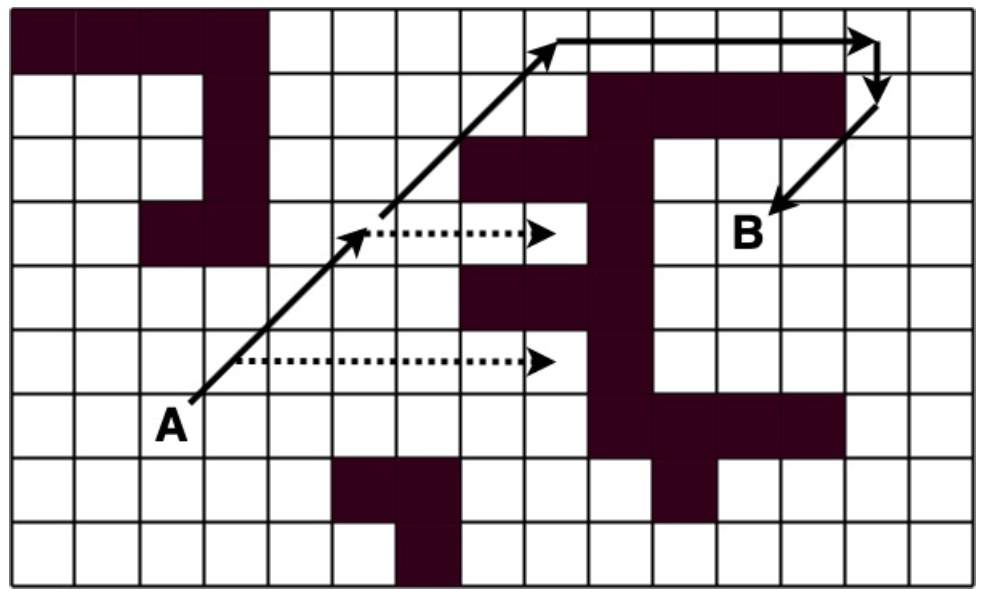
Würde man alle Nachbarn von A beginnend beim oberen Nachbar mit x0 im Uhrzeigersinn nummerieren, würden sich die Kosten des Knotens x1 (welcher sich rechts oberhalb von A befindet) wie folgt ergeben:

f(x1) = (14) + (14 ∗ 3 + 10 ∗ 6) = 116

Der Knoten x6 hätte folgendes Ergebnis:

f(x6) = (10) + (14 ∗ 3 + 10 ∗ 7) = 122

Der Knoten, welcher das niedrigste Ergebnis hat, wird für die nächste Iteration als zentraler Knoten ausgewählt und im darauf folgenden Schritt seine Nachbarn untersucht. Knoten welche als Hindernis gelten, werden bei der Evaluierung ignoriert. Zusätzlich zur Berechnung der Kosten, wird der Knoten, wessen Nachbarn untersucht werden, im Knoten x referenziert. Diese Referenz wird im Idealfall später benutzt, um den gefundenen, optimalen Weg zurückzuverfolgen. Während der Iterationen verwaltet der Algorithmus zwei Listen von Knoten - die Open-List und die Closed-List. Der Open-List werden alle untersuchten Knoten hinzugefügt. Vor der ersten Iteration befindet sich lediglich der Startknoten in der Open-List. Nach der ersten Iteration befinden sich alle begehbaren Nachbarn des Startknotens in der Open-List. In der Closed- List werden alle Knoten abgespeichert, deren Nachbarn schon untersucht wurden. Aus diesem Grund befindet sich nach der ersten Iteration der Startknoten in der Closed-List.

In der zweiten Iteration sucht der Algorithmus aus der Open-List den günstigsten Knoten heraus und beginnt wieder vom Anfang, indem er die benachbarten Felder dieses Knotens auf ihre Kosten untersucht. Dadurch dass immer eine übergreifende Liste an allen untersuchten Knoten verwaltet wird, ist es dem Algorithmus möglich aus Sackgassen hinaus zu manövrieren, wie in der Abbildung dargestellt. Wird der letzte Knoten in einer Sackgasse untersucht und der Closed-List hinzugefügt, sind noch andere, übergangene Knoten verfügbar.

Der Algorithmus endet, wenn die Open-List leer oder der untersuchte Knoten der Zielknoten ist. Im ersten Fall wären alle erreichbaren Knoten untersucht worden und zur Closed-List hinzugefügt. In so einem Fall gibt es keine Lösung. Der Zielpunkt ist nicht erreichbar. Wenn jedoch der Zielknoten erreicht wird, kann von ihm aus über die Referenzen des Vorgängerknotens auf den Startknoten zurück propagiert werden. Dadurch wird eine Liste an Knoten erstellt, welche den optimalen Pfad zum Ziel beschreiben. Der Algorithmus war in diesem Fall erfolgreich.

Eine sinnvolle Erweiterung des A*-Pathfinding-Algorithmus sind Influence-Maps. Dabei handelt es sich lediglich um eine weitere Ebene, ein weiteres Raster was zur Laufzeit aktualisiert wird. Dem entsprechend werden solche Funktionalitäten auch dahingehend implemen- tiert, dass sie speicher- und performance-sparend sind. Eine Influence-Map kann zum Beispiel dafür benutzt werden, um zu überwachen, welche Knoten für Spieler:innen einsehbar sind oder nicht. Ein weiterer Fall, ist beispielsweise, festzuhalten welche Felder in der Angriffsreichweite von gegnerischen Einheiten liegen. Diese Werte können bei jeder Iteration in die Berechnung der Kosten einbezogen werden.